LUSAS 활용
활용사례 및 기타 자료
了解和使用轴对称元素
LUSAS 활용
轴对称元素用于简化分析,只对具有轴对称特性的结构的一个截面建模,而不是对整个结构建模。
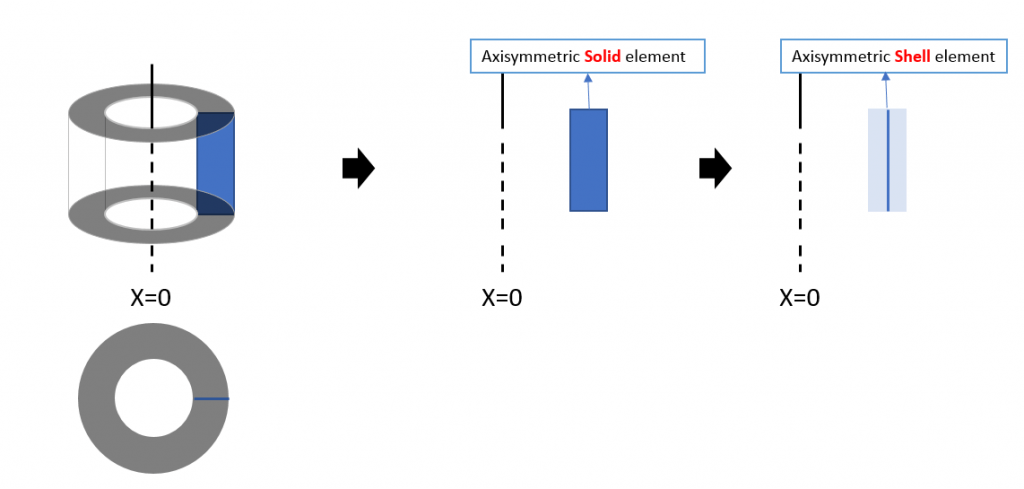
1. 轴对称载荷
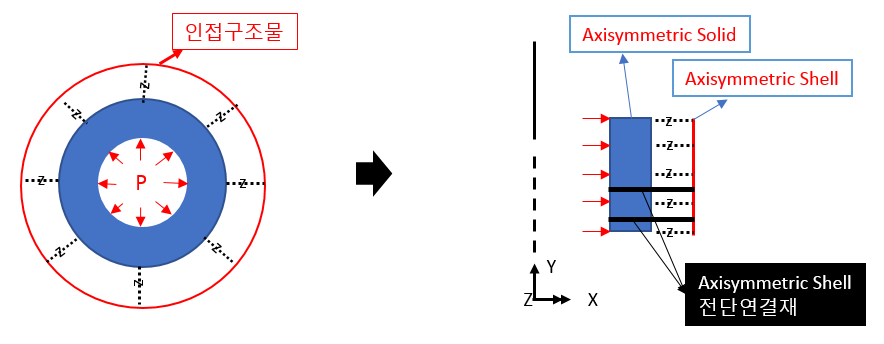
由于假定结构为轴对称结构,因此任何载荷或边界条件也假定为轴对称条件。结构的载荷条件只能在中心方向(X)和垂直方向(Y)上定义。
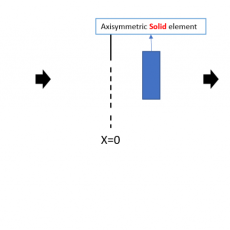
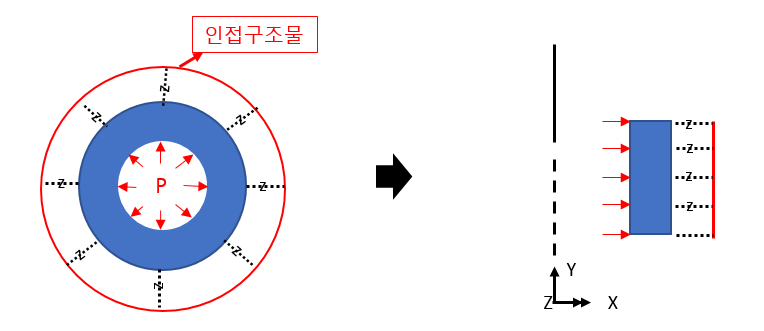
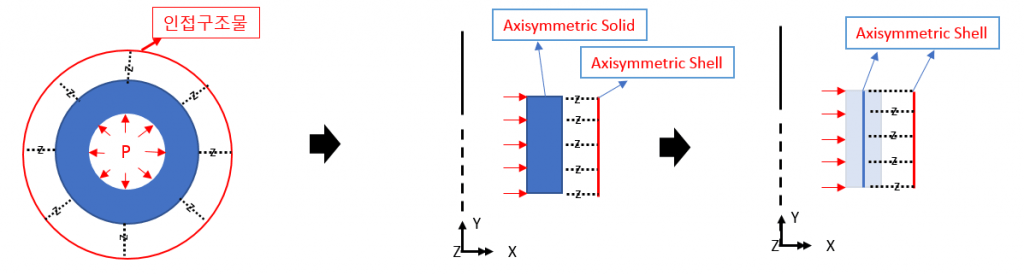
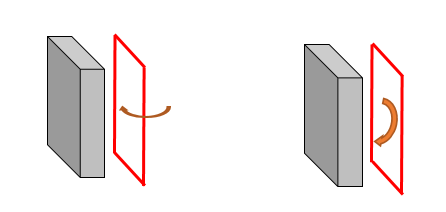
例如,在二维轴对称模型中,内压(如左图所示)被定义为施加在 Line 上的载荷(如右图所示)。
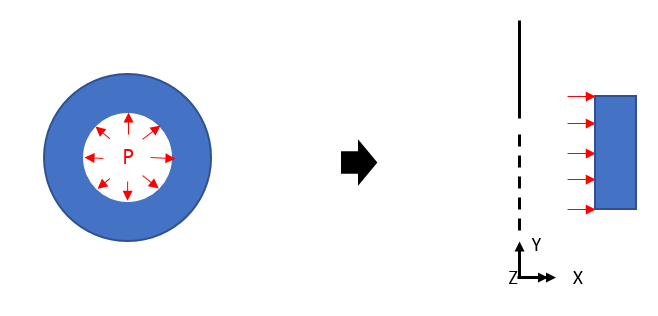
如果上述负载失效,挠度将表示为
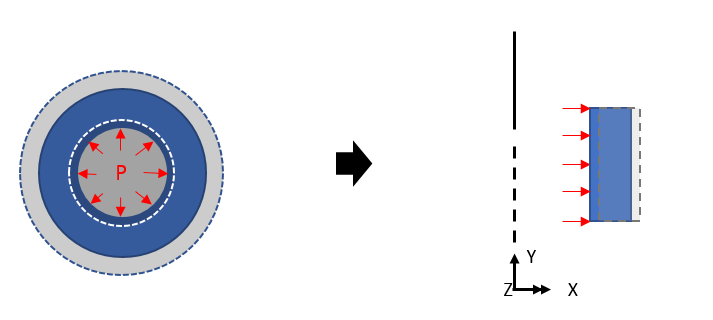
中心方向(SX)为压应力(- 号),圆周方向(SZ)为拉应力(+ 号),因为圆环被迫膨胀。

轴对称边界条件
由于假定结构为轴对称结构,因此任何载荷或边界条件也假定为轴对称施加。结构的边界条件只能在中心方向(X)和垂直方向(Y)上定义。
在模型上(下图中间位置),X 方向上的约束具有在中心方向上设置约束的效果
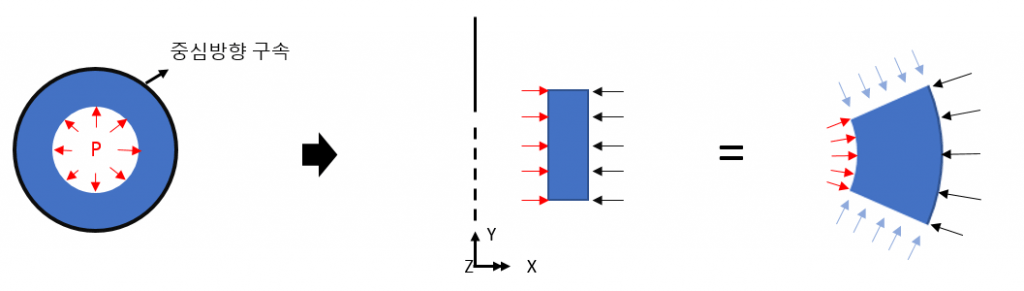
同样的概念也适用于垂直边界条件,可以根据需要进行指定。
由于圆周方向是连续结构的一个部分,因此不可能有单独的边界条件,其阻力将与材料的弹性模量成正比。
中心应力 (SX) 将产生压缩应力(- 号),而圆周应力 (SZ) 将产生压缩应力(- 号),因为结构外部受到约束并承受内部压力。
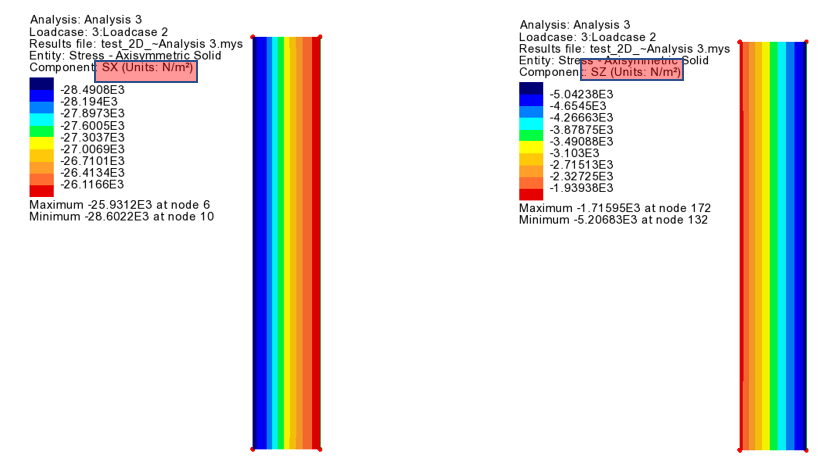
3. 结果应力方向
与上一示例一样,只能在中心(X)和垂直(Y)方向对模型施加载荷或边界条件,但也可以在圆周方向(SZ)查看应力。
4. 与邻近结构的边界条件相互作用
与相邻结构之间的相互作用可通过 “连接 “元素来表示。
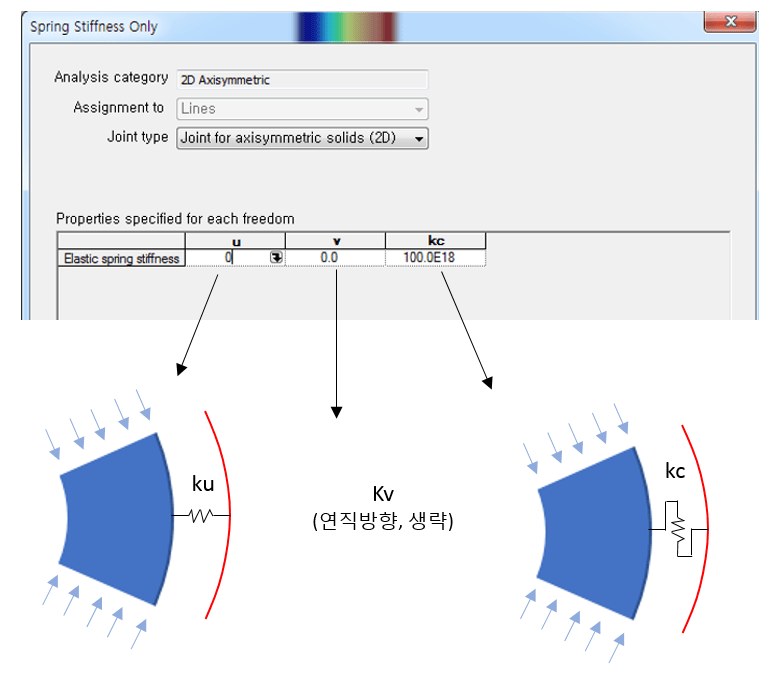
在 “连接 “元素的 “材料属性 “中,指定了每个方向的弹簧常数,以定义与相邻结构的连接特性。 轴对称结构的直接边界条件只指定了 X(中心方向)和 Y(直线方向),圆周方向的阻力与材料的弹性模量成比例,而与相邻结构的边界条件必须用弹簧表示,圆周方向没有材料模型,因此还必须指定 C(圆周,圆周方向)的条件。
请注意,由于轴对称结构的性质,指定中心方向 ku 具有限制圆周方向的效果,而无需指定圆周方向 kc。 在轴对称结构中,半径和周长成正比,因此如果中心没有位移,周长也不会有位移;如果中心受到约束,周长也会受到约束。
通过改变弹簧材料的属性类型,可以应用非线性弹簧,如抗压/抗拉弹簧、接触式弹簧、双线性弹簧等。
(1) 中心平移位移
ku 值通过放置指定的连接元素来设置。
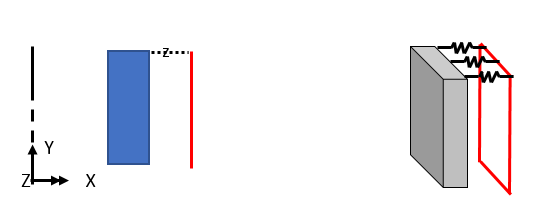
您可以通过线与线的对应关系来指定单位面积的弹簧常数。

(2) 线性平移位移
KV 值通过放置指定的连接元件来设置。

(3) 周向平移位移
Kc 值通过放置指定的连接元素来设置。

5. 与邻近结构的相互作用
如果相邻结构不是由相同的二维轴对称元素构成,而是由壳或梁元素构成,并且使用剪切连接件与相邻结构连接,则可能需要传递旋转位移。
(1) 使用轴对称壳体元素(轴对称壳体元素)
二维轴对称实体元素只有平移位移,因此无法表示力矩传递。 您也可以考虑使用 Shell 元素来解释结构。
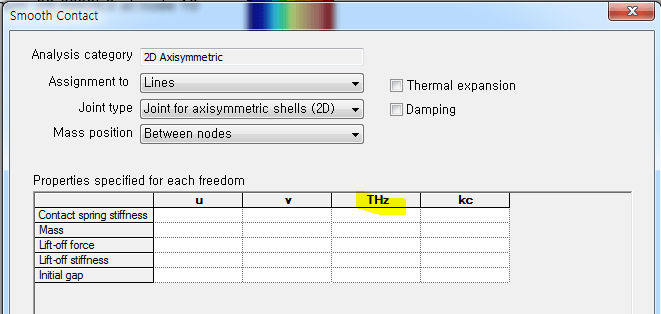
如下图所示,通过太赫兹传输的旋转位移与法线方向上的力矩引起的旋转位移相对应。
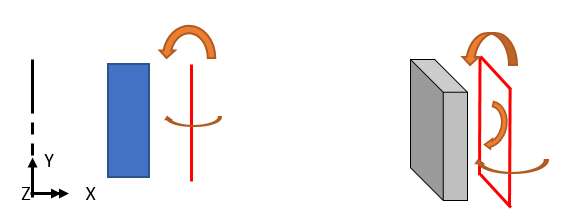
如下图所示,由于结构、载荷和边界条件均假定为轴对称,因此不存在圆周或平面内旋转位移。
如果需要考虑这些旋转位移,则需要使用三维模型,因为载荷/偏差等不是轴对称的。
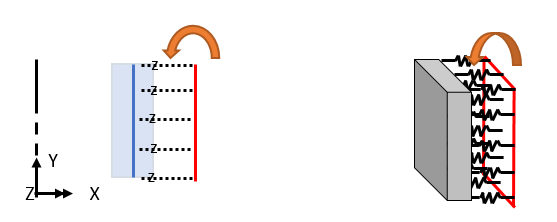
(2) 混合轴对称实体 + 轴对称壳体
由于该结构的分析模型需要同时执行(热力+结构),因此,如果需要建立厚度模型,可以考虑使用轴对称壳体元素来只实现连接(如剪切连接)。