LUSAS 활용
활용사례 및 기타 자료
축대칭 요소 이해 및 활용
LUSAS 활용
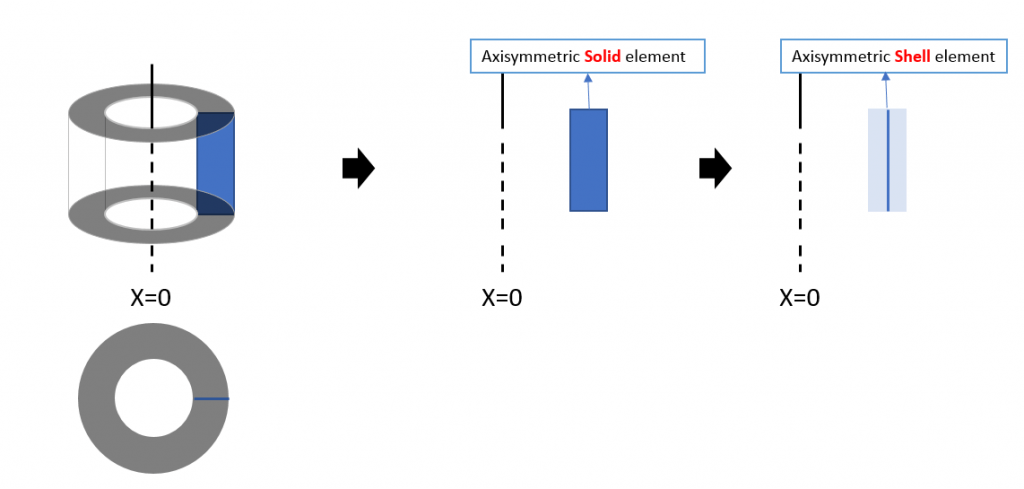
축대칭 요소는 축대칭 거동을 가지는 구조물 전체를 모델링 하는 대신 한 단면만을 모델링 하여 간편하게 해석을 진행하기 위해 사용합니다.
1. 축대칭 하중
축대칭 거동을 가정하므로, 모든 하중이나 경계조건 또한 축대칭으로 작용됨을 가정합니다. 구조물에 대한 하중조건은 중심방향 (X), 연직방향(Y) 에 대해서만 정의할 수 있습니다.
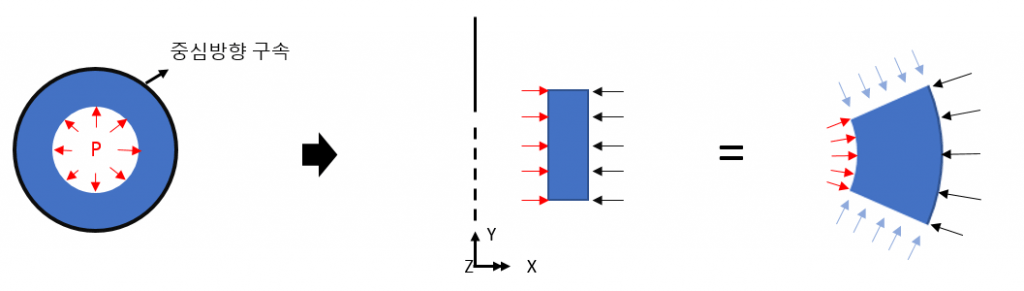
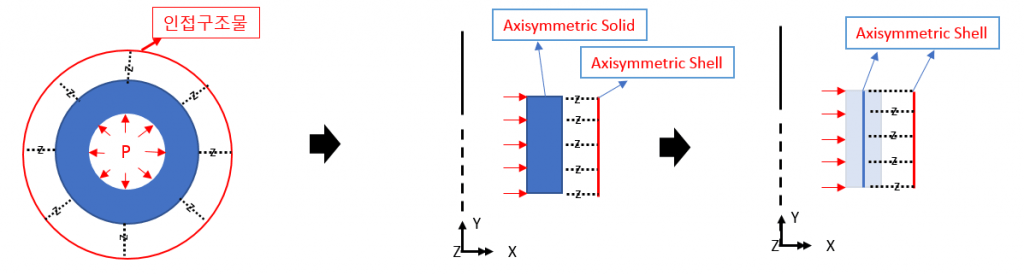
예를 들어, 좌측 그림과 같은 내압은, 우측 그림과 같이 2차원 축대칭 모델에 Line 에 적용되는 하중으로 정의됩니다.
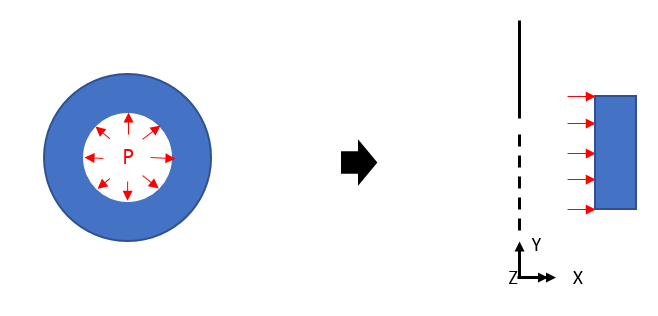
위와 같은 하중이 재해되는 경우, 처짐은 아래와 같이 표현될 것입니다.
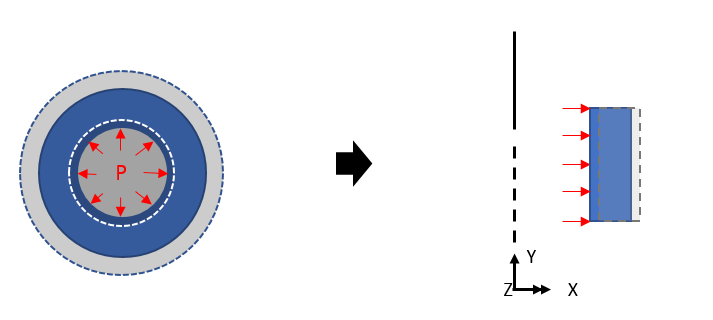
중심방향 (SX) 은 압축응력(- 부호)을 가지고, 원주방향(SZ)은 링이 강제팽창되면서 인장응력(+부호)를 가지게 됩니다.

2. 축대칭 경계조건
축대칭 거동을 가정하므로, 모든 하중이나 경계조건 또한 축대칭으로 작용됨을 가정합니다. 구조물에 대한 경계조건은 중심방향 (X), 연직방향(Y) 에 대해서만 정의할 수 있습니다.
모델상(아래 중간그림) 에서 X 방향을 구속하면, 중심방향으로 구속을 설정하는 의미를 가지게 됩니다
연직방향 경계조건도 같은 개념으로 필요에 따라 지정할 수 있습니다.
원주방향은 연속된 구조물의 한 단면이므로, 별도의 경계조건이 있을 수 없으며, 재료의 탄성계수에 비례하여 저항하게 됩니다.
중심방향 응력 (SX)는 압축응력(- 부호)를 가지게 되며, 원주방향 응력(SZ)은 구조물 바깥쪽이 구속되어 있는 상태에서 내압을 받으므로 압축응력(-부호)를 가지게 됩니다.
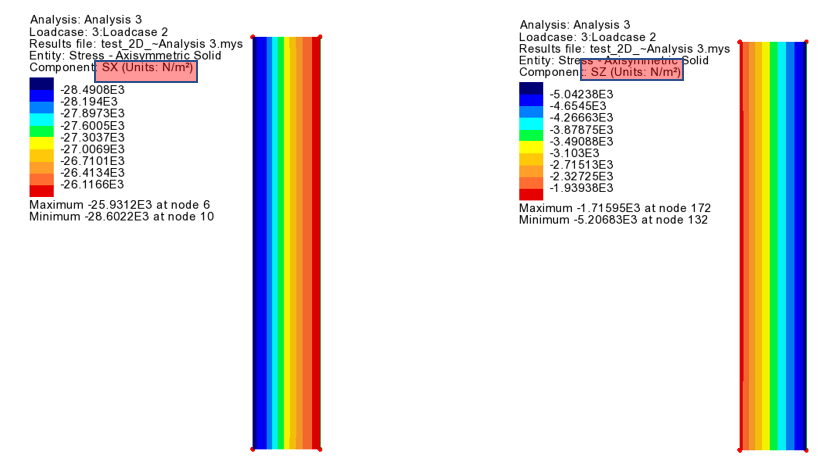
3. 결과 응력방향
앞서 예시에서와 같이, 모델상에서 하중이나 경계조건은 중심방향(X)와 연직방향(Y) 으로만 적용할 수 있으나, 응력은 원주방향(SZ) 도 확인할 수 있습니다.
4. 인접구조와의 경계조건에 의한 상호작용
인접구조와의 상호작용은 Joint 요소를 사용하여 표현할 수 있습니다.
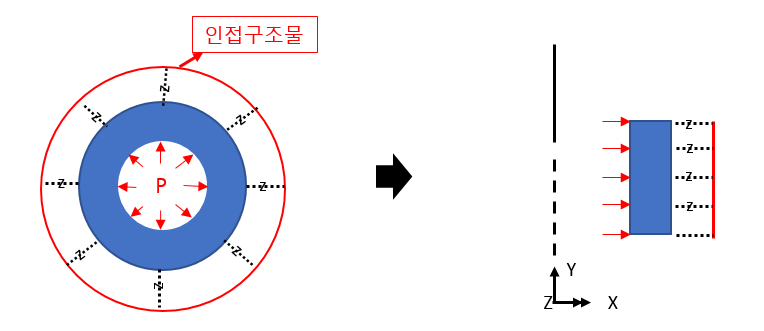
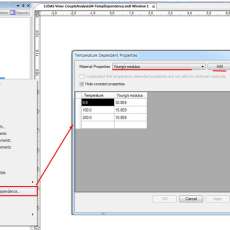
Joint 요소의 Material Property 에서 방향별 스프링 상수를 지정함으로써 인접구조물과의 연결특성을 정의하는데, 축대칭 구조에 대한 직접적인 경계조건은 X(중심방향), Y(연직방향) 만 지정하고 원주방향에 대해서는 재료의 탄성계수에 비례하여 저항하도록 되는 반면, 인접구조와의 경계조건에서는 원주방향에 대한 재료모델이 없이 스프링으로 표현되어야 하므로, C (circumferential, 원주방향)에 대한 조건도 같이 지정해야 합니다.
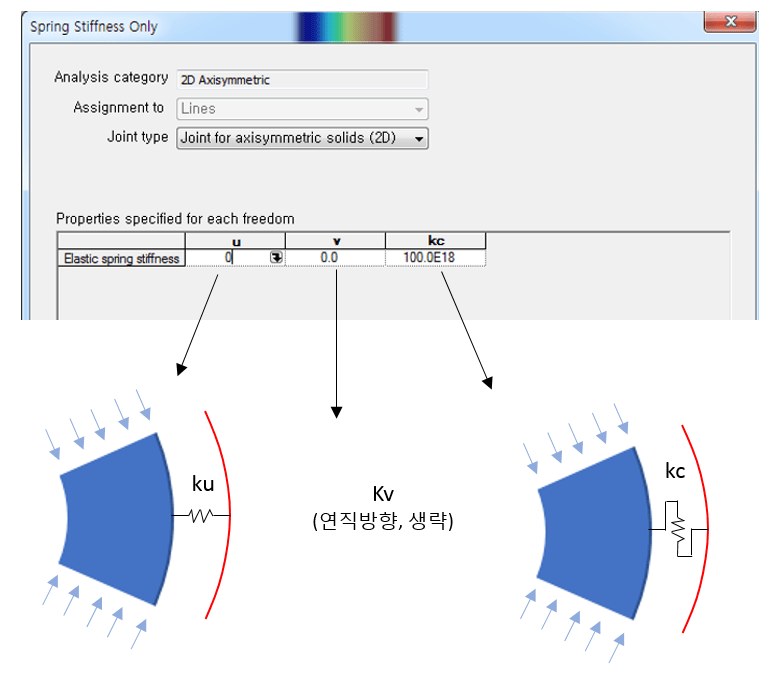
참고적으로, 축대칭 구조물의 특성상 중심방향 ku 를 지정하면, 원주방향 kc 는 지정하지 않아도 원주방향으로 구속되는 효과가 나타납니다. 축대칭 구조물은 반경과 원주길이가 비례관계에 있으므로, 중심방향의 변위가 없으면 원주방향의 변위도 없는 것과 같이, 중심방향으로 구속이 설정되면 원주방향도 구속이 되는 효과가 발생하는 것입니다.
스프링 재료특성의 종류를 변경함으로써, 압축/인장 편저항, Contact, Bilinear 등 비선형 스프링을 적용할 수 있습니다
(1) 중심방향 병진변위
ku 값을 지정한 조인트 요소를 배치함으로써 설정합니다.
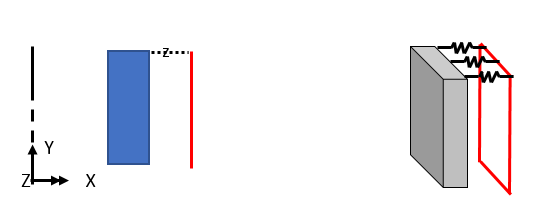
Line과 Line 을 대응시켜 단위면적당 스프링상수를 지정할 수 있습니다.

(2) 연직방향 병진변위
kv 값을 지정한 조인트 요소를 배치함으로써 설정합니다.

(3) 원주방향 병진변위
Kc 값을 지정한 조인트 요소를 배치함으로써 설정합니다.

5. 인접구조와의 연결에 의한 상호작용
인접구조물을 같은 2차원 축대칭 요소를 사용하지 않고, Shell 또는 Beam 요소를 사용하였고, 전단연결재 등이 인접구조물과의 연결에 사용되었다면, 회전변위의 전달이 필요할 수 있습니다.
(1) 축대칭 쉘 요소 사용 (Axisymmetric Shell elements)
축대칭 솔리드 모델 (2D Axisymmetric solid element)는 병진변위만을 가지고 있으므로, 모멘트 전달을 표현할 수 없습니다. 해석 대상 구조 역시 Shell 요소를 사용하는 방법을 생각해 볼 수 있습니다.
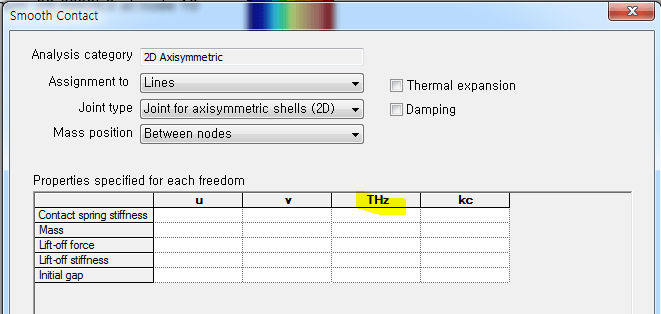
THz 를 통해 전달되는 회전변위는 아래 그림과 같이, 연직방향의 모멘트에 의해 유발되는 회전변위에 해당합니다.
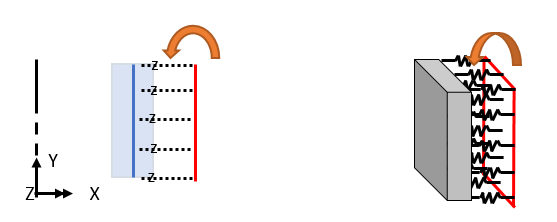
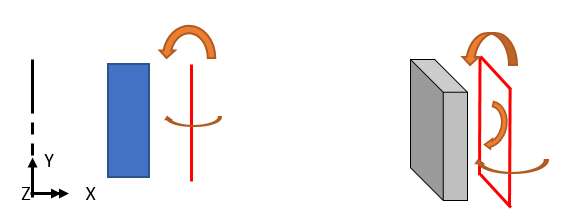
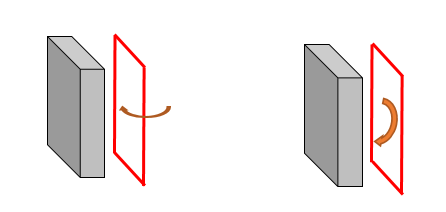
구조물, 하중, 경계조건 모두 축대칭을 가정하므로, 아래 그림과 같은 원주방향의 회전변위 또는 면내 회전변위는 발생하지 않습니다.
만약 이러한 회전변위를 고려할 필요가 있다면, 하중/처짐 등이 축대칭이 아닌 경우이므로, 3차원 모델을 사용하여야 합니다.
(2) 축대칭 솔리드 + 축대칭 쉘 혼용
본 구조물의 해석모델이 (열해석+구조해석) 을 동시에 수행해야 함에 따라, 두께를 모델링 하여야 할 필요가 있는 경우에는 연결부재 (예: 전단연결재) 만을 Axisymmetric Shell element 를 사용하여 구현하는 방법을 사용하는 방안도 생각해 볼 수 있습니다.
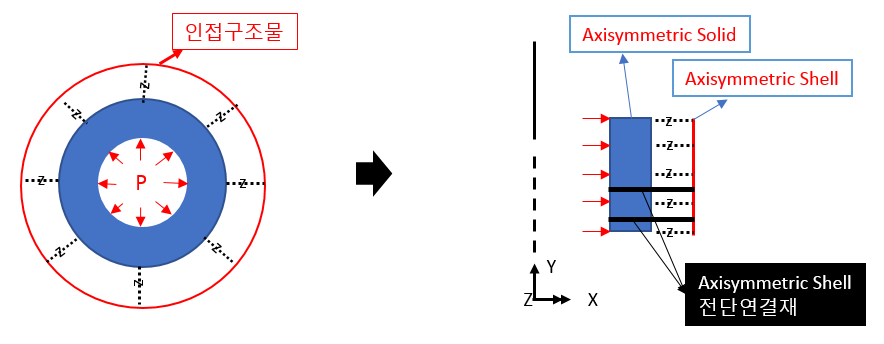
통상 연결재는 원주방향으로 연속성을 가진 축대칭 구조물은 아니겠으나, 원주방향으로 연속성을 가지는 Axisymmetric Shell 요소로 모사하고, 원래의 단면제원 혹은 탄성계수를 사용하는 대신, 원래 연결재의 방향별 강도가 축대칭으로 모델링 된 상태에서도 동일한 수준을 발현하도록 등가의 두께/탄성계수를 환산하여 적용하여야 합니다.
시공단계별 해석은 이전 단계의 처짐과 응력상태를 초기조건으로 하여 다음 단계에서 구조물이 추가되거나 하중이 추가되는 형태로 해석을 수행하는 비선형 해석입니다.
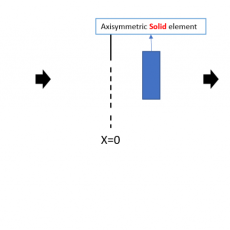
축대칭 요소는 축대칭 거동을 가지는 구조물 전체를 모델링 하는 대신 한 단면만을 모델링 하여 간편하게 해석을 진행하기 위해 사용합니다. 축대칭 요소를 사용하는 구조해석에서 하중, 경계조건, 결과추출 관련된 내용을 정리합니다.